티스토리 뷰
반응형
4.1 Introduction
우리는 여태까지 하나의 문항에 답을 하는 것을 보았다.
그러나 총 테스트에서 몇 점을 받았는지, 총 테스트가 어떤지는 다루지 않았다.
만약 이 시험을 치른 사람들이 다시 이 문제를 기억하지 못한다면, 이 문제를 다시풀면 이 난이도의 문제는 특정 평균 근처에 모일 것이다. 이 값은 진점수(true score)이라고 한다.
4.2 A True Score
같은 능력에 있는 사람들의 진점수를 봐보자. 능력을 1이라 생각하고 진점수를 계산해보자.
문항모수를 다음과 같이 정해보자.
문항1:
문항2:
문항3:
문항4:
위의 값을 모두 더하면
TS = 2.617934906
4.3 The Test Characteristic Curve

능력에 따라 진점수를 얼마 받을지의 그래프로 바뀌었다.
만약 1.0에 선을 그리면 그 값은 2.62가 나올 것이다.
4.4 Computer Session
b= [-1.0,0.75,0.0,0.5]
a=[0.5,1.2,0.8,0.75]
theta = np.arange(-3,3.1,0.1)
ts = np.repeat(0,len(theta))
J=len(b)
for j in range(J):
P=1/(1+np.exp(-a[j]*(theta-b[j])))
ts=ts+P
plt.plot(theta,ts)
plt.xlabel('Ability')
plt.ylabel('True Score')
plt.xlim(-3,3)
plt.ylim=(0,J)
plt.show()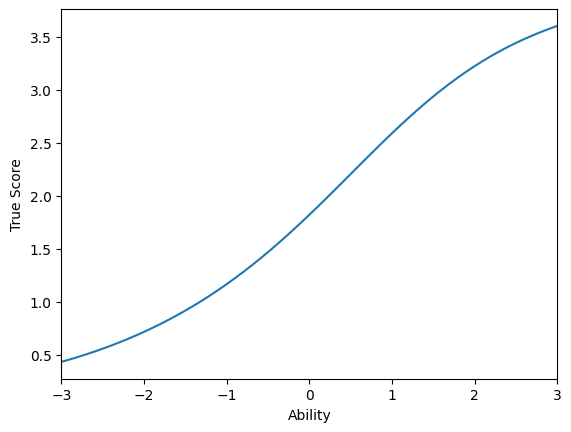
시험 특성 곡선을 그려보았다.
그냥 사실 원래 구하던 함수에 값을 넣고 더한 것 밖에 특별한 것은 없다.
함수화하기
def tcc(b,a=np.repeat(1,J),c=np.repeat(0,J)): # 리스트로 받아야함
J=len(b)
theta = np.arange(-3,3.1,0.1)
ts = np.repeat(0,len(theta))
J=len(b)
for j in range(J):
P=1/(1+np.exp(-a[j]*(theta-b[j])))
ts=ts+P
plt.plot(theta,ts)
plt.xlabel('Ability')
plt.ylabel('True Score')
plt.xlim(-3,3)
plt.ylim=(0,J)
plt.yticks([i for i in range(1,J+1)])
plt.title('Test Characteristic Curve')
plt.plot()
plt.show()b=[-2.0,-1.0,0.0,1.0,2.0]
a=[0.5,0.75,1.0,0.75,0.5]
tcc(b,a)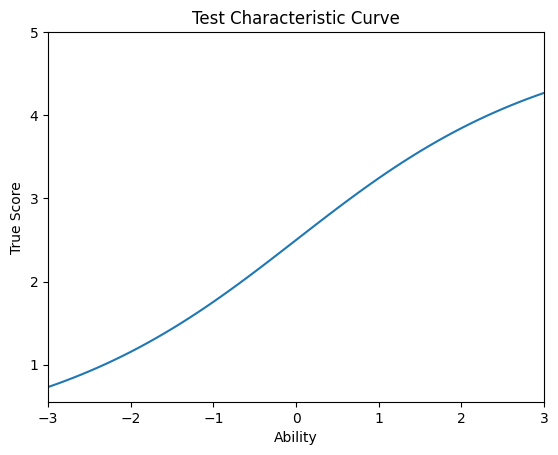
책에는 안나왔지만 능력에 따라 위치를 찾아주는 것도 구현해봤다.
def tcc(b,a=np.repeat(1,J),c=np.repeat(0,J),ability=1): # 리스트로 받아야함
J=len(b)
theta = np.arange(-3,3.1,0.1)
ts = np.repeat(0,len(theta))
J=len(b)
for j in range(J):
P=1/(1+np.exp(-a[j]*(theta-b[j])))
ts=ts+P
plt.plot(theta,ts)
plt.xlabel('Ability')
plt.ylabel('True Score')
plt.xlim(-3,3)
plt.ylim=(0,J)
plt.yticks([i for i in range(1,J+1)])
plt.title('Test Characteristic Curve')
ts2=0
for j in range(J):
P=1/(1+np.exp(-a[j]*(ability-b[j])))
ts2=ts2+P
tss=np.arange(0,ts2,0.01)
abil=[ability +i*0 for i in tss]
plt.plot(abil,tss,'--')
plt.show()b=[-2.0,-1.0,0.0,1.0,2.0]
a=[0.5,0.75,1.0,0.75,0.5]
tcc(b,a,ability=-2)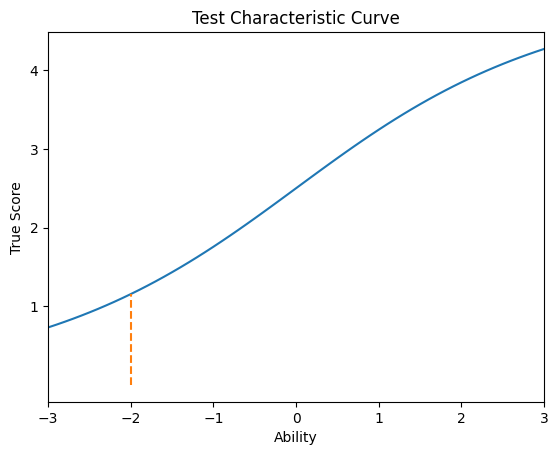
반응형
'심리학 > 문항반응이론' 카테고리의 다른 글
| [Basic of IRT using R] 6. The Information Function (1) | 2024.01.23 |
|---|---|
| [Basic of IRT using R] 5. Estimating an Examinee's Ability (0) | 2024.01.18 |
| [Basic of IRT using R] 3. Estimating Item Parameters (1) | 2024.01.14 |
| [Basic of IRT using R] 2. Item Characteristic Curve Models (2) | 2024.01.11 |
| [Basic of IRT using R] 1. The item Characteristic Curve (1) | 2024.01.09 |
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 사회심리학
- 코딩테스트
- c++
- 류근관
- K-MOOC
- 인프런
- Python
- 파이썬
- 회계
- 열혈프로그래밍
- jlpt
- 일문따
- 강화학습
- 일본어
- C
- 일본어문법무작정따라하기
- C/C++
- 보세사
- 백준
- 정보처리기사
- 티스토리챌린지
- 여인권
- 오블완
- 인지부조화
- 심리학
- 윤성우
- 데이터분석
- stl
- 뇌와행동의기초
- 통계학
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
글 보관함
반응형

