티스토리 뷰
Baker, F. B., & Kim, S. H. (2017). The basics of item response theory using R (pp. 17-34). New York: Springer.
문항반응이론을 R로 밑바닥부터 구현한 책을 찾았다.
이 책의 코드를 파이썬으로 바꿔서 구현을 해보자.
1.1 Introduction
교육학 혹은 심리학에서 관심의 대상이 되는 변수들이 있다.
예를 들어, 지능, 흥미 등 이런 변수들은 직관적으로 이해가 되지만 측정은 또 다른 일이다.
비슷하게 '능력(ability)' 또한 직관적으로 '수학을 잘한다.' 영어를 잘한다' 등은 이해가 되지만 이를 측정하는 것은 또 별개의 문제가 된다. 이러한 눈으로 볼 수 없는 능력이나 흥미의 대상을 우리는 잠재변인(latent variable)이라고 한다.
하지만 물리적인 특성(키, 몸무게 등)과 달리 이런 능력은 직접적으로 측정할 수 없다.
일반적으로 이를 검사하기 위해 문항(예를 들어 질문)을 만들고 이에 대한 대답을 들을 수 있다. 고전적 검사 이론에서는 '정답 수/문제 수'로 능력을 측정했지만 이는 문제가 있다. 왜냐하면 수능문제의 난이도를 '정답 수/문제 수'의 관점에서 본다면, 초등학생이 시험을 본 경우 난이도는 10이 된다면, 수능 만점자만 모아서 시험을 본다면 매우 난이도가 낮을 수 있다. 문항 반응이론은 이러한 고전검사의 문제를 해결하기 위해 응시자의 능력과 난이도를 함께 고려한다.
1.2 The item characterisitic curve

문항특성곡선(The itme characteristic curve)은 능력에 따른 난이도를 같이 쓰고 있다.
기본적으로 x축은 능력을 의미하고 \(\theta\)로 쓴다. -3에 가까울수록 능력이 낮은 것이며 y축(정답을 맞출 확률)이 낮아진다. 반대로 오른쪽, 3쪽으로 갈수록 능력은 높아지고 정답을 맞출 확률은 올라간다.
'고전 검사 이론'에서는 '맞춘 갯수/ 전체 갯수'로 난이도를 측정했다면,
'문항 반응 이론'에서는 '1개의 문항'에서의 난이도와 정답확률을 보여준다.
1.3 Item Difficulty and Item Discrimination

위의 그래프를 자세히 살펴보자.
y축은 정답을 맞출 확률
x축은 개인의 능력을 나타낸다.
세 개의 곡선이 보이는데 각가의 위치가 다르다.
맨 아래에 있는 그래프는 개인의 능력이 높은 구간(3에 가까울수록)과 낮은구간(-3에 가까울수록)에서 모두 정답을 맞출 능확률이 낮다.
공부의 예시를 든다면, 공부를 잘하는 학생이나 공부를 못하는 학생이나 다 못풀었기 때문에 이는 어려운 문항이 된다.
반대로 맨 위의 문항은 모두 확률이 높은데 이는 쉬운 문항이 된다.

위의 그래프를 보면 그래프의 기울기가 가파라지는 지점이 있다.
일정 능력 이상이면 모두 맞추지만, 일정 능력 이하라면 맞추지 못하는 문제라 볼 수 있다.
이는 변별도가 높은 문항으로 볼 수 있는데 '합격/불합격'과 같은 선발에서도 사용될 수 있다.
1.4 Verbal Terms of Item Difficulty and Item Discrimination
문항의 난이도는 말로써 정의할 수도 있는데 다음과 같이 할 수도 있다.
1)매우쉬움
2) 쉬움
3) 보통
4) 어려움
5) 매우 어려움
또는 변별도를 나타낼 수도 있는데
1) 없다
2) 낮다
3) 중간
4) 높다
5) 완벽
1.5 Computer session
파이썬을 사용하여 위에서 보았던 문항반응이론의 그래프를 그려보자.
먼저 개인의 능력(\(\theta\)를 만든다.
theta = np.arange(-3,3.1,0.1)
thetaarray([-3.00000000e+00, -2.90000000e+00, -2.80000000e+00, -2.70000000e+00,
-2.60000000e+00, -2.50000000e+00, -2.40000000e+00, -2.30000000e+00,
-2.20000000e+00, -2.10000000e+00, -2.00000000e+00, -1.90000000e+00,
-1.80000000e+00, -1.70000000e+00, -1.60000000e+00, -1.50000000e+00,
-1.40000000e+00, -1.30000000e+00, -1.20000000e+00, -1.10000000e+00,
-1.00000000e+00, -9.00000000e-01, -8.00000000e-01, -7.00000000e-01,
-6.00000000e-01, -5.00000000e-01, -4.00000000e-01, -3.00000000e-01,
-2.00000000e-01, -1.00000000e-01, 2.66453526e-15, 1.00000000e-01,
2.00000000e-01, 3.00000000e-01, 4.00000000e-01, 5.00000000e-01,
6.00000000e-01, 7.00000000e-01, 8.00000000e-01, 9.00000000e-01,
1.00000000e+00, 1.10000000e+00, 1.20000000e+00, 1.30000000e+00,
1.40000000e+00, 1.50000000e+00, 1.60000000e+00, 1.70000000e+00,
1.80000000e+00, 1.90000000e+00, 2.00000000e+00, 2.10000000e+00,
2.20000000e+00, 2.30000000e+00, 2.40000000e+00, 2.50000000e+00,
2.60000000e+00, 2.70000000e+00, 2.80000000e+00, 2.90000000e+00,
3.00000000e+00])
그리고 난이도, 변별도인 b(bmedium)와 a(amodeerate)를 만든다.
bmedium=0
amoderate=1
p=1/(1+np.exp(-amoderate*(theta-bmedium)))
plt.plot(theta,p)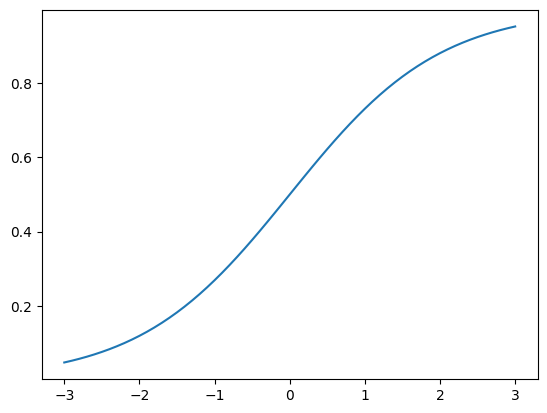
여기에 레이블을 더해보자.
plt.plot(theta,p)
plt.xlabel('theta')
plt.ylabel('p')
plt.show()
1.5.2 A Function for Item Charateristic Curves
위에서 썼던 코드를 하나의 함수로 만들어서 여태까지 해온 일을 해보자.
def iccplot(b,a): ## b는 난이도, a는 변별도
theta = np.arange(-3,3.1,0.1)
p=1/(1+np.exp(-a*(theta-b)))
plt.plot(theta,p)
plt.xlabel("Ability")
plt.ylabel('Probability of Correct response')
plt.ylim(0,1)
plt.xlim(-3,3)
plt.yticks([0,0.5,1])
plt.show()
이제 난이도와 변별도를 넣어서 필요할 때마다 만들 수 있다.
iccplot(0,1)
이제 난이도를 쉽고 어렵고 혹은 변별도가 있고 없고에 따라 코딩을 해보자.
#난이도
bveryeasy=-2.625
beasy=-1.5
bmedium=0
bhard=1.5
bveryhard=2.625anone=0
alow=0.4
amoderate=1
ahigh=2.1
aperfect=999그래프를 그려보자.
iccplot(bmedium,amoderate) #난이도 중간, 변별도 중간
iccplot(beasy,amoderate) #난이도는 쉽고, 변별도 중간
1.6 Exercises
1.낮은 항목 난이도와 높은 항목 식별도를 가진 아이템을 그래프로 표현하려 합니다.
(a) iccplot 함수를 사용하여 쉬운 항목 난이도와 높은 항목 식별도를 가진 아이템의 특성 곡선을 그립니다.
-> 난이도(b)는 낮고, 식별도(a)는 높은 그래프를 그린다.
iccplot(beasy,ahigh)

(b) 그래프에서 대부분의 능력 범위에서 정답 확률이 상당히 높을 것으로 보입니다. 아이템 특성 곡선은 능력 범위의 하부 에서 급격할 것입니다.
(c) 곡선을 연구한 후 R 콘솔 창을 클릭하여 해당 창을 현재 창으로 만들고 새로운 명령 행을 입력합니다. (d) 다음 그래프는 새로운 그래픽 창에 플로팅됩니다.
2.높은 항목 난이도와 낮은 항목 식별도를 가진 아이템을 그래프로 표현하려 합니다.
(a) iccplot 함수를 사용하여 어려운 항목 난이도와 낮은 항목 식별도를 가진 아이템의 특성 곡선을 그립니다.
(b) 그래프에서 대부분의 능력 범위에서 정답 확률이 전반적으로 낮을 것으로 보입니다. 아이템 특성 곡선은 그리 급격하지 않을 것입니다.
(c) 곡선을 연구한 후 R 콘솔 창을 클릭하여 해당 창을 현재 창으로 만들고 새로운 명령 행을 입력합니다. (d) 다음 그래프는 새로운 그래픽 창에 플로팅됩니다.
iccplot(bhard,alow)

3.중간 항목 난이도와 낮은 항목 식별도를 가진 아이템을 그래프로 표현하려 합니다.
(a) iccplot 함수를 사용하여 중간 항목 난이도와 낮은 항목 식별도를 가진 아이템의 특성 곡선을 그립니다.
(b) 그래프에서 능력 범위 내에서 정답 확률이 0.2에서 0.8 사이에 있을 것으로 보입니다. 아이템 특성 곡선은 사용된 능력 범위에서 거의 선형일 것입니다.
(c) 곡선을 연구한 후 R 콘솔 창을 클릭하여 해당 창을 현재 창으로 만들고 새로운 명령 행을 입력합니다.
(d) 다음 그래프는 새로운 그래픽 창에 플로팅됩니다.
iccplot(beasy,alow)

4. 이 연습에서는 모든 항목이 동일한 항목 난이도를 가지지만 서로 다른 수준의 항목 식별도를 갖습니다. 목적은 곡선의 가파름을 항목 식별도의 수준과 관련시키는 것입니다.
(a) iccplot 함수를 사용하여 중간 항목 난이도와 적당한 항목 식별도를 가진 아이템의 특성 곡선을 그립니다.
(b) 그래프에서 낮은 능력 수준에서 정답 확률이 작고 높은 능력 수준에서 크게 나타날 것으로 보입니다. 아이템 특성 곡선은 능력 범위의 중간 부분에서 적당히 가파를 것입니다.
(c) 곡선을 연구한 후 R 콘솔 창을 클릭하여 해당 창을 현재 창으로 만들고 새로운 명령 행을 입력합니다.
(d) 다음 그래프는 동일한 그래픽 창에 플로팅됩니다. (e) 다음 명령을 입력하세요:
par(new=T) (f)
이제 중간 항목 난이도를 사용하여 각 항목에 대해 선택한 항목 식별도 수준 (예: 없음, 낮음, 높음, 완벽)을 사용하여 단계 a에서 d까지 여러 번 반복하십시오.
(g) 다음 그래프는 새로운 그래픽 창에 플로팅됩니다.
def iccplot2(b,a): ## b는 난이도, a는 변별도
theta = np.arange(-3,3.1,0.1)
p=1/(1+np.exp(-a*(theta-b)))
plt.plot(theta,p,label=f'b={b}, a={a}')
plt.xlabel("Ability")
plt.ylabel('Probability of Correct response')
plt.ylim(0,1)
plt.xlim(-3,3)
plt.legend()
plt.yticks([0,0.5,1])
iccplot2(bmedium,amoderate)
iccplot2(bmedium,anone)
plt.show()함수를 좀 수정했다.

5. 이 연습에서는 모든 항목이 동일한 항목 식별도를 가지지만 서로 다른 수준의 항목 난이도를 갖습니다. 목적은 항목이 능력 척도상의 위치를 항목 난이도의 수준과 관련시키는 것입니다.
(a) iccplot 함수를 사용하여 매우 쉬운 항목 난이도와 적당한 항목 식별도를 가진 아이템의 특성 곡선을 그립니다.
(b) 그래프에서 대부분의 능력 척도에서 정답 확률이 상당히 크게 나타날 것으로 보입니다. 아이템 특성 곡선은 능력 척도의 하부에서 적당히 가파를 것입니다.
(c) 곡선을 연구한 후 R 콘솔 창을 클릭하여 해당 창을 현재 창으로 만들고 새로운 명령 행을 입력합니다.
(d) 다음 그래프는 동일한 그래픽 창에 플로팅됩니다.
(e) 다음 명령을 입력하세요:
par(new=T) (f) 이제 중간 항목 식별도를 사용하여 각 항목에 대해 선택한 항목 난이도 수준 (예: 쉬움, 중간, 어려움, 매우 어려움)을 사용하여 단계 a에서 d까지 여러 번 반복하십시오.
(g) 다음 그래프는 새로운 그래픽 창에 플로팅됩니다.
iccplot2(bveryeasy,amoderate)
iccplot2(bmedium,amoderate)
plt.show()
6. 원하는 항목 난이도 및 항목 식별도 조합으로 여러 실험을 진행하여 선택한 수준에 대응하는 항목 특성 곡선의 모양을 예측할 수 있을 때까지 실험해보세요. 컴퓨터에서 화면에 표시되기 전에 예상한 곡선의 개략적인 스케치를 그릴 경우 도움이 될 수 있습니다.
'심리학 > 문항반응이론' 카테고리의 다른 글
| [Basic of IRT using R] 4. The Test characteristic curve (0) | 2024.01.16 |
|---|---|
| [Basic of IRT using R] 3. Estimating Item Parameters (1) | 2024.01.14 |
| [Basic of IRT using R] 2. Item Characteristic Curve Models (2) | 2024.01.11 |
| 2. The one-parameter Model (1) | 2023.11.15 |
| 1. Introduction to Measurement (0) | 2023.11.05 |
- Total
- Today
- Yesterday
- 보세사
- 정보처리기사
- 심리학
- 오블완
- 통계학
- 백준
- 파이썬
- 일본어문법무작정따라하기
- C
- stl
- 강화학습
- c++
- K-MOOC
- 뇌와행동의기초
- C/C++
- 일문따
- 행동심리학
- 통계
- 조건형성
- 일본어
- 코딩테스트
- 회계
- 인지부조화
- Python
- 열혈프로그래밍
- 류근관
- 사회심리학
- 티스토리챌린지
- 윤성우
- 데이터분석
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |

