티스토리 뷰
1.2-1. A boy found a bicycle lock for which the combination was unknown. The correct combination is a four-digit
number, d1d2d3d4, where di, i = 1, 2, 3, 4, is selected from 1, 2, 3, 4, 5, 6, 7, and 8. How many different lock
combinations are possible with such a lock?
1.2-1. 어떤 소년이 알 수 없는 자전거 자물쇠를 발견했습니다. 올바른 조합은 d1d2d3d4로, 여기서 di, i = 1, 2, 3, 4는 1, 2, 3, 4, 5, 6, 7, 8 중에서 선택됩니다. 이러한 자물쇠로는 몇 가지 서로 다른 조합이 가능한가요?
\(8^4\)
=4096
1.2-2. In designing an experiment, the researcher can often choose many different levels of the various factors
in order to try to find the best combination at which to operate. As an illustration, suppose the researcher is
studying a certain chemical reaction and can choose four levels of temperature, five different pressures, and two
different catalysts.
(a) To consider all possible combinations, how many experiments would need to be conducted?
(b) Often in preliminary experimentation, each factor is restricted to two levels. With the three factors noted,
how many experiments would need to be run to cover all possible combinations with each of the three factors
at two levels? (Note: This is often called a 23 design.)
1.2-2. 실험 설계 시 연구자는 여러 요인의 여러 수준을 선택하여 가장 효과적인 조합을 찾을 수 있습니다. 예를 들어, 어떤 화합물 반응을 연구하는 연구자가 온도에 대해 네 가지 수준, 압력에 대해 다섯 가지 수준, 그리고 촉매에 대해 두 가지 수준을 선택할 수 있다고 가정해 봅시다. (a) 모든 가능한 조합을 고려하려면 몇 번의 실험을 수행해야 할까요? (b) 종종 예비 실험에서 각 요인을 두 수준으로 제한합니다. 세 가지 요인에 대해 모든 가능한 조합을 포함하려면 각각의 세 요인에 대해 몇 번의 실험이 필요할까요?
(a) 4 x 5 x 2 = 40
(b) 2 x2x2 =8
1.2-3. How many different license plates are possible if a state uses
(a) Two letters followed by a four-digit integer (leading zeros are permissible and the letters and digits can be
repeated)?
(b) Three letters followed by a three-digit integer? (In practice, it is possible that certain “spellings” are ruled
out.)
1.2-3. 만약 어떤 주가 다음과 같은 규칙을 사용한다면 가능한 라이선스 플레이트는 몇 가지일까요? (a) 두 개의 문자 뒤에 네 자리 정수 (앞에 0이 올 수 있고, 문자와 숫자를 반복 사용할 수 있음)? (b) 세 개의 문자 뒤에 세 자리 정수? (실제로는 특정한 "맞춤법"이 제외될 수 있습니다.)
(a)
10 x 10 x 10 x 10 x 26 x 26
(b)
10x10x10x26x26x26
1.2-4. The “eating club” is hosting a make-your-own sundae at which the following are provided:
| Ice Cream Flavors | Toppings |
| Chocolate | Caramel |
| Cookies ‘n’ cream | Hot fudge |
| Strawberry | Marshmallow |
| Vanilla | M&M’s |
| Nuts | |
| Strawberries |
(a) How many sundaes are possible using one flavor of ice cream and three different toppings?
(b) How many sundaes are possible using one flavor of ice cream and from zero to six toppings?
(c) How many different combinations of flavors of three scoops of ice cream are possible if it is permissible to make all three scoops the same flavor?
(a) 하나의 아이스크림 풍미(flavor)와 세 가지 다른 토핑을 사용하여 가능한 선데는 몇 가지인가요?
\( 4 \times _{6}\mathrm{C}_{3} =80\)
(b) 하나의 아이스크림 풍미와 0에서 6까지의 토핑을 사용하여 가능한 선데는 몇 가지인가요?
\( 4 \times (_{6}\mathrm{C}_{0} + _{6}\mathrm{C}_{1} + _{6}\mathrm{C}_{2} + _{6}\mathrm{C}_{3} + _{6}\mathrm{C}_{4} + _{6}\mathrm{C}_{5} + _{6}\mathrm{C}_{6}) =256 \)
(c) 세 스쿱의 아이스크림의 다양한 풍미의 조합이 가능하며, 세 스쿱이 모두 동일한 풍미일 수 있는 경우는 몇 가지인가요?
4가지
1.2-5. How many four-letter code words are possible using the letters in IOWA if
(a) The letters may not be repeated?
(b) The letters may be repeated?
(a) 4! = 24
(b) \(4^4=256\)
1.2-6. Suppose that Novak Djokovic and Roger Federer are playing a tennis match in which the first player to win
three sets wins the match. Using D and F for the winning player of a set, in how many ways could this tennis match
end?
FFF = 1
DFFF 4!/3! -1 = 3
DDFFF 5!/2!3! -(4!3!-1) =7
=10 x2( 다른 쪽이 승리도 있음)
1.2-7. In a state lottery, four digits are drawn at random one at a time with replacement from 0 to 9. Suppose that you win if any permutation of your selected integers is drawn. Give the probability of winning if you select
(a) 6, 7, 8, 9.
(b) 6, 7, 8, 8.
(c) 7, 7, 8, 8.
(d) 7, 8, 8, 8.
(a)
\( \frac{4!}{10^4}\)
(b)
\(\frac{4!/2!}{10^4}\)
(c)
\(\frac{\frac{4!}{2!2!}}{10^4}\)
(d)
\(\frac{\frac{4!}{3!}}{10^4}\)
1.2-8. How many different varieties of pizza can be made if you have the following choice: small, medium, or large
size; thin ‘n’ crispy, hand-tossed, or pan crust; and 12 toppings (cheese is automatic), from which you may select
from 0 to 12?
\(3 \times 3 \times 2^{12} =36684\)
(사이즈 3개, 얇기 3개, 토핑12개(이항정리에 의하여 0개부터 12개까지 선택가능))
1.2-9. The World Series in baseball continues until either the American League team or the National League team
wins four games. How many different orders are possible (e.g., ANNAAA means the American League team wins
in six games) if the series goes
(a) Four games?
(b) Five games?
(c) Six games?
(d) Seven games?
(a)
2 (아메리카 이김, 네셔녈 이김)
(b)
ANNNN -> 2 x (5!/4!) - 2(4대 떡 승리) =10
(c)
AANNNN -> 2 x 6!/2! - 8 -2 (4대 떡 승리, 4대1승리) = 20
(d)
AAANNNN -> 2 x 7!(3!4!) - 20 -8 - 2(4대떡, 4대1, 4대2 승리 빼기) = 40
1.2-10. Pascal’s triangle gives amethod for calculating the binomial coefficients; it begins as follows:

The nth row of this triangle gives the coefficients for (a + b)n−1. To find an entry in the table other than a 1 on the boundary, add the two nearest numbers in the row directly above. The equation
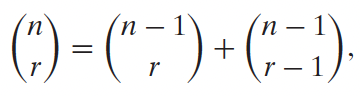
called Pascal’s equation, explains why Pascal’s triangle works. Prove that this equation is correct.
증명문제는 생략한다...
1.2-11. Three students (S) and six faculty members (F) are on a panel discussing a new college policy.
(a) In how many different ways can the nine participants be lined up at a table in the front of the auditorium?
(b) How many lineups are possible, considering only the labels S and F?
(c) For each of the nine participants, you are to decide whether the participant did a good job or a poor job
stating his or her opinion of the new policy; that is, give each of the nine participants a grade of G or P.
How many different “scorecards” are possible?
(a) 9!=362880
(b) 9!/(3!6!) = 84
(c) \(2^9 = 512\) 이항정리에 의해서
1.2-12. Prove

.
Hint: Consider (1 − 1)^n and (1 + 1)^n, or use Pascal’s equation and proof by induction.
증명은 우선 생략
1.2-13. A bridge hand is found by taking 13 cards at random and without replacement from a deck of 52 playing
cards. Find the probability of drawing each of the following hands.
(a) One in which there are 5 spades, 4 hearts, 3 diamonds, and 1 club.
(b) One in which there are 5 spades, 4 hearts, 2 diamonds, and 2 clubs.
(c) One in which there are 5 spades, 4 hearts, 1 diamond, and 3 clubs.
(d) Suppose you are dealt 5 cards of one suit, 4 cards of another. Would the probability of having the other
suits split 3 and 1 be greater than the probability of having them split 2 and 2?
(a)
\( \frac{ _{13}\mathrm{C}_{5} \times _{13}\mathrm{C}_{4} \times _{13}\mathrm{C}_{3} \times _{13}\mathrm{C}_{1} }{_{52}\mathrm{C}_{13}}\)
(b)
\( \frac{ _{13}\mathrm{C}_{5} \times _{13}\mathrm{C}_{4} \times _{13}\mathrm{C}_{2} \times _{13}\mathrm{C}_{2} }{_{52}\mathrm{C}_{13}}\)
(c)
\( \frac{ _{13}\mathrm{C}_{5} \times _{13}\mathrm{C}_{4} \times _{13}\mathrm{C}_{1} \times _{13}\mathrm{C}_{3} }{_{52}\mathrm{C}_{13}}\)
(d)
'통계학 > Hogg 확률과 통계적 추론' 카테고리의 다른 글
| 1-4. 독립사상 문제풀이 (0) | 2024.03.15 |
|---|---|
| 1-3 조건부확률 (1) | 2024.02.27 |
| 1-1 연습문제 풀이 (1) | 2024.02.24 |
| 1.2 경우의 수 (1) | 2024.02.24 |
| 제1장 확률 (0) | 2024.02.22 |
- Total
- Today
- Yesterday
- 보세사
- 열혈프로그래밍
- 일본어
- 파이썬
- c++
- 심리학
- 윤성우
- 학습심리학
- 강화학습
- 데이터분석
- 티스토리챌린지
- 통계
- 행동주의
- 오블완
- 코딩테스트
- 류근관
- 일문따
- 인지부조화
- 행동심리학
- 통계학
- 정보처리기사
- 일본어문법무작정따라하기
- 조건형성
- Python
- 회계
- 물류정책기본법
- 백준
- K-MOOC
- C
- 물류관리사
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |

